Computer as physics object

ЗАНЯТИЕ 5. 04.10.02

Компьютер как физический объект.

1. Компакт-диск как дифракционная решетка

2. Размер одного бита

3. КПД процессора

4. Скейлинг системы охлаждения

§0. Введение.

В процессе изучения физики человек постепенно осознает, что физика - это не правила игры, по которым положено решать задачи и получать точные ответы, а способ мышления, позволяющий объяснять те или иные явления в реальном мире. При этом особую важность приобретает умение сопоставлять наблюдаемые факты с конкретной формулировкой того или иного физического закона. По мере обучения осознается также вторая сторона той же медали - умение не только найти проявление физического закона в реальном мире, но и изготовить прибор, механизм или устройство, демонстрирующее или использующее конкретную физическую закономерность, то есть создать определенную технологию. В конце концов, именно этого ждет человеческое сообщество от физики. Понятно, что современные технологии основаны на огромном количестве закономерностей, (хотя они все равно проще, чем некоторые проявления живой природы), однако изготовленное людьми всегда можно разделить на отдельные части и выделить ту или иную закономерность, проявляющуюся в них. На этом занятии мы попытаемся это сделать на примере всем известного персонального компьютера. Конечно, мы не сможем, да и не успеем рассмотреть все стороны его работы, но кое-что легко объяснить даже на школьном уровне физики.

§1. Компакт-диск как дифракционная решетка

Начнем с рассмотрения обычного компакт-диска. Как он устроен?

Визуальный осмотр позволяет утверждать, что поверхность компакт-диска состоит из множества концентрических окружностей. Логично предположить, что каждая окружность - дорожка, модуляция параметров которой (толщины, глубины, коэффициента отражения) как раз и содержит информацию, записанную на диске.

Следующий вопрос - какова ширина одной полоски? Разумно предположить, что все они имеют одинаковую ширину. Тогда достаточно легко ее измерить: малый кусочек поверхности диска представляет собой дифракционную решетку, работающую на отражение. Направляя на диск обычную лазерную указку, легко в этом убедится: кроме отраженного пучка легко видеть несколько дифракционных максимумов. Теперь можно измерить период дифракционной решетки: измеряя угол между нулевым и первым дифракционными максимумами, по стандартной формуле находим .

Стандартные объемы современных компакт-дисков - 650, 700 и 800 мегабайт (последние пока что находятся в стадии разработки и не поступили в широкую продажу). Для ширин дорожек получаем результаты, показанные в первой половине таблицы 1. В процессе вычисления учитывалось, что для лазерной указки , а . Как и следовало ожидать, ширина одной дорожки всего в несколько раз больше длины волны и уменьшается с увеличением емкости компакт-диска. Отсюда естественным образом вытекает вопрос - до каких пор можно увеличивать емкость компакт-диска?

Таблица 1.

, Mb	, см	, см		,	, см	, см	, cм²	,
650	112±1	260±2	0.40	1.625	2.2	5.9	94.2	0.64
700	117±1	260±2	0.41	1.585	2.2	5.9	94.2	0.61
800	135±3	260±2	0.46	1.413	2.2	5.9	94.2	0.60

§2. Размер одного бита

Теперь, когда мы измерили ширину дорожек, логично предположить, что на одной дорожке биты информации располагаются один за другим. При этом размер одного бита не может быть существенно меньше длины волны, что связано с дифракционными ограничениями. Однако мы не знаем длины волны, на которой работает CD-ROM. Попытаемся ее измерить. Предположим, что площадь, занимаемая одним битом, имеет порядок . Измеряя внутренний и внешний радиусы компакт-диска, найдем площадь его рабочей поверхности (она одинакова у всех дисков) и разделим ее на ширину дорожки и количество битов , учитывая, что каждый байт в целях контроля четности на самом деле содержит не 8, а 14 битов. Результаты показаны во второй части таблицы 1. Легко видеть, что эффективные длины волн для всех трех дисков оказываются практически одинаковыми, что подтверждает, что наши предположения близки к истине. Теперь мы можем ответить на вопрос о возможностях увеличения емкости компакт-диска: без уменьшения длины волны, на которой работает CD-ROM, увеличение емкости диска может быть достигнуто только за счет уменьшения ширины дорожек. Однако ширину дорожек также нельзя делать менее длины волны, что означает, что максимально возможное увеличение объема компакт-диска - примерно в 3 раза, до 2 гигабайт, то есть возможности хранения информации на оптических дисках использованы практически полностью. Действительно, преимущества DVD-технологии связаны с использованием многослойных покрытий, содержащих до 10 независимых слоев, содержащих информацию.

Попробуем теперь обсудить тот же вопрос для магнитных способов хранения информации, например, для жестких дисков. Характерные пространственные масштабы в этом случае определяются уже не длиной световой волны, а постоянной кристаллической решетки, то есть минимальный размер одного бита имеет порядок введенного на первом занятии типичного расстояния между атомами . Современные винчестеры имеют плотность записи порядка 10 гигабит на квадратный дюйм, то есть реальный размер одного бита оказывается порядка . Таким образом, биты на современных магнитных носителях информации оказываются примерно на три порядка больше, чем в принципе могли бы. Задумаемся, какие еще физические причины ограничивают снизу размеры одного бита.

Очевидно, что при магнитной записи любой бит - это маленький домен ферромагнитного вещества, имеющий два состояния намагниченности, соответствующих нулю и единице. Однако при уменьшении размеров домена энергия, запасенная в нем за счет намагниченности, уменьшается. С другой стороны, тепловая флуктуация способна изменить намагниченность некоторой области домена, размер которой называется радиусом корреляции. При температуре Кюри, при которой ферромагнетик становится парамагнетиком, этот радиус стремится к бесконечности. При уменьшении температуры радиус корреляции тоже уменьшается. Таким образом, энергии тепловой флуктуации достаточно для того, чтобы полностью изменить намагниченность домена размерами менее радиуса корреляции. Это ограничение размеров одного бита называется в технологии изготовления винчестеров парамагнитным пределом. Произведем грубую оценку величины парамагнитного предела вдали от температуры Кюри. Магнитный момент одной кристаллической ячейки разумно взять равным магнитному моменту электрона, называемом магнетоном Бора

Энергия взаимодействия магнитных моментов соседних кристаллических ячеек тогда будет иметь порядок

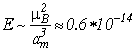эрг,

то есть энергия домена, состоящего из нескольких кристаллических ячеек, уже сравнима с энергией тепловых флуктуаций при комнатной температуре эрг. Однако для реально использующихся материалов парамагнитный предел составляет 80 гигабит на квадратный дюйм, то есть не менее на один бит, а возможности увеличения плотности записи информации связывают с развитием технологий использования многослойных магнитных покрытий.

Q06< Не связаны ли ограничения на плотность записи на винчестер со сложностью создания достаточно малой записывающе-считывающей головки?

A06< Современные сканирующие туннельные микроскопы используют острия, позволяющие создавать электрическое поле или регистрировать его с площадки не более 10нм в диаметре, так что принципиальных проблем с созданием достаточно малых головок не должно быть.

§3. КПД процессора

Какие еще причины могут ограничивать возможности компьютера? Как минимум один аспект мы до сих пор не затрагивали – это энергетические соображения. Рассмотрим, на что тратится мощность, потребляемая самой активной частью компьютера – процессором.

В конечном итоге, любая операция, производимая процессором, заключается в изменении состояния одной или нескольких ячеек – ячейки процессора, памяти или винчестера. А каждая ячейка, так или иначе, представляет собой потенциальную яму с двумя минимумами, то есть имеющая два устойчивых состояния, соответствующих нулю и единице. Для переключения ее состояния необходимо затратить как минимум энергию, превышающую потенциальный барьер, разделяющий две ямы. Может ли этот барьер сделать сколь угодно малым? Очевидно – нет, в любом случае он должен превышать энергию тепловых флуктуаций, иначе ячейка будет менять свое состояние сама по себе. В реальности напряжение работы процессора порядка нескольких вольт (наиболее экономичные модели процессоров для ноутбуков потребляют ровно один вольт), то есть электрон, который перекидывают из ямы в яму под действием этого напряжения, получает энергию эрг, то есть на два порядка больше при комнатной температуре.

Полная полезная энергия, потребляемая процессором, определяется как энергией, расходуемой на одну операцию, так и их количеством. Быстродействие последних моделей процессоров практически однозначно определяются его частотой: процессор, работающий на частоте , совершает примерно операций в секунду. Таким образом, минимальная мощность, требующаяся процессору, имеет порядок , что на 11 порядков меньше реально потребляемой мощности!

Осталось выяснить, на что же уходит потребляемая энергия. Помимо нагрева окружающего пространства, у процессора, пожалуй, есть еще только один канал потери энергии – это излучение электромагнитных волн. Тактовые частоты работы процессоров находятся в том же диапазоне, что и частоты связи сотовых и радиотелефонов. Чтобы проверить, способен ли работающий процессор внести помехи в телефонные разговоры, оценим мощность энергии, излучаемой процессором. Процессор, работающий на частоте и напряжении , потребляет мощность примерно . Отсюда ток , а его производная . Мощность, излучаемая переменным током, согласно формулам электродинамики [ЛЛ II], определяется как

что на 5 порядков больше минимальной мощности, но на 6 меньше реально потребляемой. В то же время характерные мощности сотовых и радиотелефонов составляют и , соответственно, то есть излучение процессора не может создать серьезных помех телефонной связи. Что касается всей остальной энергии, потребляемой процессором, то она преобразуется в тепло, и вентилятор вынужден ее отводить, чтобы процессор не перегрелся.

Q07< Как учесть энергию, уходящую на переключение емкостей полупроводниковых переходов?

A07< Поскольку емкости не поглощают энергию, а только запасают ее, нам не обязательно их учитывать при рассмотрении баланса энергии.

§4. Скейлинг системы охлаждения

Чтобы рассмотреть эффективность работы вентилятора, сформулируем простую задачу: пусть у нас есть процессор, потребляющий 25 ватт, который охлаждается вентилятором, потребляющим 1 ватт. Допустим, что мы заменили процессор более мощным, потребляющим в два раза больше энергии. Во сколько раз при этом должна возрасти мощность вентилятора для того, чтобы без изменения геометрических размеров он охлаждал процессор до той же температуры, что и раньше?

Из-за вязкости воздуха вблизи поверхности процессора всегда есть слой, скорость которого достаточно мала для того, чтобы теплоперенос в нем осуществлялся преимущественно за счет теплопередачи. Из законов гидродинамики [ЛЛ VI] следует, что характерная толщина слоя пропорциональна корню из скорости воздуха вдали от процессора, а поток энергии в нем пропорционален градиенту температуры. Так как по условиям задачи температура процессора не должна измениться, перепад температур в слое должен остаться прежним, поэтому для того, чтобы поток энергии вырос в два раза, необходимо уменьшить толщину слоя в два раза, то есть увеличить скорость воздуха в четыре.

Но энергия, которую вентилятор сообщает воздуху за единицу времени, определяется как произведение объема воздуха на энергию единицы объема воздуха, разгоняемого до этой скорости, то есть мощность процессора определяется по следующей формуле:

то есть для увеличения скорости воздуха в четыре раза мощность процессора должна возрасти в 64 раза - для охлаждения процессора мощностью 50 ватт потребуется вентилятор мощностью 64 ватта, и его самого надо будет охлаждать.

Q08< Как меняет эффективность охлаждения теплопроводящая паста между процессором и радиатором?

A08< Поскольку паста занимает место воздушной прослойки, а ее собственная теплопроводность достаточно велика, то увеличение потока отводящегося тепла определяется отношением теплопроводностей металла и воздуха, которое по порядку величины равно .

P23. Для компакт-диска:

а). оценить максимально возможную скорость вращения.

б). измерить реальную скорость вращения в CD-ROM.

а). Центробежные силы способны оторвать молекулу от диска, если при перемещении молекулы на атомное расстояние они совершат работу, равную атомной энергии:

откуда

c^-1.

На самом деле, несомненно, диск вращается значительно медленнее. Отчасти, это связано с тем, что информацию, снятую с него, еще нужно успеть прочитать. Быстродействие современных фотодетекторов обычно не превышает наносекунды, а время, за которое необходимо произвести считывание одного бита, обратно пропорционально частоте вращения:

откуда максимальная частота вращения

кГц,

или 100000 оборотов в минуту.

б). Измерим теперь реальную частоту вращения компакт-дисков. Как известно, однократная скорость вращения компакт-диска соответствует скорости передачи данных 150 кб/с, откуда для частоты вращения получаем 200 об/мин для внешних дорожек и 530 об/мин - для внутренних. Казалось бы, это означает, что для наиболее скоростных 52-х-скоростных приводов CD-ROM частота вращения меняется от 10400 до 27660 оборотов в минуту, то есть превышает скорость вращения винчестеров.

Произведем непосредственные измерения. Измерения производились при помощи пишущего привода CD-RW TEAC 32´8´4. Воспользовавшись тем, что запись на диск всегда начинается с внутренних дорожек, запишем файл размеров 100 Мб на болванку, засекая время записи, далее заполним почти весь ее объем чем-нибудь еще и снова запишем файл размером 100 Мб. Затем измерим время считывания обоих файлов.

Результаты измерения приведены в таблице:

Время

записи, с

Скорость

вращения

Время

чтения, с

Скорость

вращения

Внутренние

дорожки

7.9

15.5

Внешние

дорожки

8.1

30.3

Таким образом, скорость записи оказывается постоянной, то есть частота вращения падает при возрастании диаметра дорожки, тогда как при чтении скорость записи внешних дороже оказывается в два раза больше, что означает практически постоянную частоту вращения.

Оказывается, это связано с современной технологией изготовления CD-ROM: частота вращения компакт-диска является переменной при скоростях записи-чтения не более 12-ти-кратных, но постоянной - при больших скоростях. В нашем случае запись производится с 8-ми-кратной скоростью, при которой CD-ROM изменяет частоту вращения, обеспечивая постоянство скорости записи. В то же время, чтение происходит с большими скоростями, поэтому CD-ROM фиксирует частоту вращения, обеспечивая 30-ти-кратную скорость записи на внешних дорожках, но только 16-ти-кратную - на внутренних. Таким образом, если у вас есть 52-х-кратный CD-ROM, то это означает 52-х-кратную скорость только на внешних дорожках, на внутренних же она примерно в два раза меньше.