Задачи (в скобках указана стоимость задачи в баллах)

 

1. (1) На оси собирающей линзы, имеющей оптическую силу  диоптрий, находится объект. Определить, с какой скоростью будет двигаться его изображение, если линза двигается вдоль оси с постоянной скоростью . Может ли эта скорость быть больше скорости света?

 

Решение:

Направим ось  вдоль оптической оси линзы и поместим объект в начало координат. Тогда положения линзы  и изображения объекта  связаны формулой тонкой линзы

, откуда .

Дифференцируя полученное выражение, получаем скорость изображения:

.

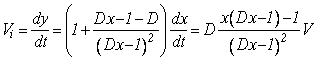Когда расстояние от линзы до объекта близко к фокусному , эта скорость стремится к бесконечности. Несомненно, ничто не мешает ей превысить скорость света, так как при этом не происходит переноса энергии или передачи информации - аналогично ситуации с солнечным зайчиком.

 

2. (3) Трамвайные провода протягиваются не по прямой, а "зигзагом" (если смотреть сверху). Зачем?

 

Решение:

В отличие от троллейбусов, у трамваев сверху всего один провод, который играет роль “фазы”. Роль “земли” при этом играют рельсы. Если бы провод был параллелен рельсам, он бы прикасался к металлической штанге, снимающей напряжение, в одном и том же месте, и постепенно пропиливал бы в ней канавку. Для того, чтобы избежать перепиливания штанги, провод натягивают зигзагом.

 

3*. (3) Аспирант Саша показывает студентам Паше и Наташе установку, в которой лазерный луч отражается зеркалом. "Саша, - говорит Паша, глядя на пучок, - у тебя очень плохое зеркало. Смотри, падает много, а отражается мало." "Да нет, - говорит Наташа, - совсем наоборот. Падает мало, а отражается много." Объясните физику этого явления.

 

Решение:

Если студенты видят пучок, значит, в воздухе имеются пылинки, на которых пучок упруго рассеивается. Однако диаграмма направленности такого рассеяния однородна лишь в случае, когда размер неоднородностей (пылинок) много меньше длины волны. Если же размер пылинок больше длины волны, рассеяние происходит в основном вперед. Поэтому можно сделать такие выводы:

1) Паша смотрит навстречу падающему пучку, а Наташа – навстречу отраженному;

2) Размер пылинок в комнате - порядка нескольких микрон.

 

4. (3) Вы пришли на автобусную остановку и увидели, что автобус только что ушел. Каково наиболее вероятное время появления следующего автобуса, если они приходят совершенно независимо друг от друга со средней частотой  автобусов в единицу времени?

 

Решение:

Найдем вероятность того, что за время  к остановке прибудет  автобусов. Такая вероятность определяется биномиальным распределением

,

где вероятность  появления каждого автобуса пренебрежимо мала , но общее число  автобусов на трассе стремится к бесконечности, причем среднее значение  остается конечным. При таких приближениях биномиальное распределение сводится к распределению Пуассона:

.

Отсюда легко находим вероятность того, что за время  не прибудет ни одного автобуса:

,

так что наиболее вероятное время прибытия следующего автобуса , тогда как среднее время прибытия следующего автобуса .

 

5. Фотодетектор преобразует свет, падающий на него, в последовательность электронных фотоимпульсов. Частота появления фотоимпульсов в каждый момент времени пропорциональна интенсивности света. Если источником света служит лазерный луч, то дисперсия числа появляющихся за некий интервал времени фотоимпульсов равна их среднему значению: . Оценить дисперсию числа фотоимпульсов, если источником света служит:

а). (3) периодически мигающий лазер;

б). (5) одинокий возбужденный атом.

 

Решение:

а). Как отмечено в решении задачи 7б, задача о фотодетектировании с математической точки зрения эквивалентна задаче о потоке машин, поэтому распределение числа фотоотсчетов в случае падения на фотодетектор лазерного света с постоянной интенсивностью  определяется распределением Пуассона (см. задачу 4):

,

где  - эффективность фотодетектора. Если лазер мигает с периодом  и скважностью , то средние значения числа и квадрата числа импульсов

,

,

откуда дисперсия

.

Обычно  и вторым членом можно пренебречь.

б). Одинокий возбужденный атом может излучить один фотон и перейти в основное состояние. Чтобы он излучил следующий фотон, его нужно снова возбудить, что в любом случае займет некоторое время. Поэтому вероятность того, что за малое время фотодетектор зарегистрирует два фотона, строго равна нулю. Это означает, что дисперсия числа фотоотсчетов , т.е. меньше, чем в случае падения на фотодетектор лазерного света с постоянной эффективностью. Этот парадоксальный результат носит название эффекта антигруппировки фотонов и строго обосновывается только в рамках квантовой оптики.

 

6*. (3) При рассеянии луча лазера в мутной среде (растворе молока или куске полиэтилена) возникает спекл-структура, состоящая из отдельных пятен. Оценить средний размер пятен на экране, находящемся на расстоянии метра от мутной среды.

 

Решение:

Спекл-структура - результат интерференции лучей, рассеянных отдельными частицами (или неоднородностями) рассеивающей среды. Разность оптических путей лучей, рассеянных под углом , по порядку величины равна , где  - расстояние между рассеивателями. Электрические поля этих двух лучей будут складываться в фазе, если эта разность не больше длины волны. Отсюда получаем угловой размер отдельного пятна спекл-структуры:

,

где  - максимально возможное расстояние между рассеивателями, т.е. диаметр лазерного пучка. Для размера пятен спекл-структуры, находящейся на расстоянии метра от рассеивающей среды, на которой рассеивается луч гелий-неонового лазера  диаметром , получаем:

 

7. На широкой улице к перекрестку, перед которым стоит светофор, независимо друг от друга подъезжают машины. Красный свет на светофоре горит в течение времени . Найти вероятность того, что к моменту, когда загорится "зеленый", перед светофором стоит  машин, в двух случаях:

а). (3) среднее число машин , подъезжающих к светофору в единицу времени, постоянно;

б). (5) среднее число машин, подъезжающих к светофору в единицу времени, описывается произвольной функцией .

 

Решение:

а). Как было показано в задаче 4, вероятность того, что за время  к светофору подъедут  машин, определяется распределением Пуассона:

.

б). В случае, когда плотность потока машин является переменной функцией, параметр распределения Пуассона также все время меняется. За бесконечно малый промежуток времени  может прийти одна или ноль машин с вероятностями  и , соответственно. Поэтому, если  - вероятность появления  машин за время , то

.

Отсюда получаем, что набор функций  описывается системой дифференциальных уравнений

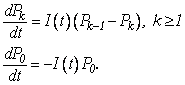
Решение этой системы, как можно доказать по индукции, имеет вид распределения Пуассона

,

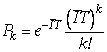где  - среднее за время  значение плотности потока машин. Однако в различные интервалы горения красного света функция , вообще говоря, различна. Для того, чтобы учесть это, необходимо усреднить полученное распределение по всем возможным значениям средней плотности :

,

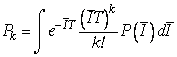где  - функция распределения средней плотности потока машин, т.е.  -вероятность того, что средняя плотность находится в диапазоне . Полученная формула в классической теории фотодетектирования называется формулой Манделя, так как наша задача с математической точки зрения эквивалентна задаче о вероятности появления  фотоотсчетов на фотодетекторе, который освещен светом с интенсивностью .

 

8*. (5) Луч неподвижного лазера необходимо направить так, чтобы он проходил через две маленькие дырочки. Однако у экспериментатора нет зеркал - есть только неограниченное количество стеклянных треугольных призм двух типов: равносторонних и равнобедренных прямоугольных, а также стеклянные плоскопараллельные пластинки произвольной толщины. Каков алгоритм, позволяющий направить лазерный луч через дырочки с минимальными потерями его интенсивности (поглощением в стекле можно пренебречь)?

 

Решение:

Основные потери интенсивности лазерного пучка будут вызваны отражениями от граней оптических элементов, поэтому необходимо использовать минимальное их количество. С помощью плоскопараллельной пластины произвольной толщины можно параллельно сместить луч на любое расстояние, а с помощью прямоугольной призмы – повернуть пучок на 90°. При этом потери на отражение будут минимальными, так как угол падения можно сделать точно равным нулю для призмы и почти равным нулю – для пластины. Равносторонняя (шестидесятиградусная) призма позволяет повернуть пучок на угол, отличный от 90°, но при этом потерь можно избежать лишь для одной поляризации (за счет использования угла Брюстера). В общем случае будем использовать только первые два типа элементов.

Возможны три варианта взаимного расположения исходного луча и прямой, соединяющей две дырочки:

1) Они параллельны. Можно использовать одну пластину или две 90-градусные призмы (в первом случае потери будут меньше).

2) Они не лежат в одной плоскости. Можно использовать две 90-градусные призмы.

3) Они пересекаются. Тогда нужно сначала перевести луч в другую плоскость, сместив его пластиной, а затем воспользоваться двумя 90-градусными призмами.

 

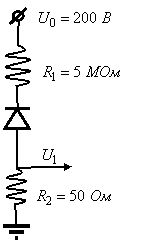
9. (5) Для регистрации отдельных фотонов используют лавинный фотодиод. Для этого диод включается по схеме, изображенной на рисунке. В темноте диод "заперт" и не пропускает ток. При попадании на диод одного фотона возникает электронная лавина и его внутреннее сопротивление резко уменьшается до . В результате с сопротивления  снимается импульс , который имеет очень короткий () передний фронт и очень пологий () задний. Объяснить такую асимметрию фронта импульса.

 

Решение:

У фотодиода имеется собственная емкость , величина которой составляет несколько пикофарад (точное значение, впрочем, для решения задачи не требуется). После попадания фотона эта емкость начинает разряжаться через диод, сопротивление которого равно . Время этого процесса составляет с, если принять пф. Когда напряжение на диоде падает, он перестает проводить, и емкость заряжается уже через сопротивление . Время этого процесса составляет с. Поэтому соотношение длин переднего и заднего фронтов импульса определяется отношением .

 

10. (1) “Круги на воде”

“Чукча стоит на мосту и кирпичи в воду бросает. К нему подходит прохожий:

- Ты зачем кирпичи в воду бросаешь?

- Пытаюсь понять, однако, почему кирпич квадратный, а круги по воде круглые?”

Внимание, вопрос: а какую форму на самом деле имеют круги от брошенного в воду прямоугольного кирпича?

 

Решение:

Согласно принципу Гюйгенса-Френеля, для нахождения формы кругов на воде необходимо найти форму огибающей волновых фронтов всех возбужденных волн. Если считать, что кирпич касается поверхности воды одновременно всей своей поверхностью, то в первый момент времени фронт будет иметь форму прямоугольника. При дальнейшего его эволюции участки плоских волн останутся плоскими, а от углов кирпича будут расходится дуги окружностей. Таким образом, “круги” на воде будут иметь форму отрезков, равных сторонам кирпича, соединенных дугами окружностей, и на расстоянии, много большем размеров кирпича, будут иметь практически круглую форму.

---

* Элементы описанных в задачах экспериментальных схем находятся у организаторов олимпиады, при желании их можно подержать в руках для лучшего понимания физики ситуаций.