Задачи (в скобках указана стоимость задачи в баллах) и их решения:

 

1 *. В лаборатории с полки на пол свалился ящик, наполненный как поляроидами, так и просто стеклянными пластинками.

a (1) Как отделить осколки поляроидов от простых стеклянных осколков?

b) (3) Как быть в случае, если поляроидов было очень мало?

Решение:

Для того, чтобы отличить поляроид от простого темного стекла, надо пропустить через него поляризованный свет: интенсивность прошедшего света будет зависеть от ориентации поляроида.

Если возможно найти второй поляроид – то свет, вышедший из него, будет поляризованным, поэтому интенсивность света, прошедшего через два поляроида, зависит от угла между ними по закону Малюса.

Если второго поляроида нет, то для получения частично поляризованного света достаточно посмотреть на любую отражающую поверхность под большим углом – вследствие различия коэффициентов Френеля для разных поляризаций одна из них отражается значительно сильнее, чем другая.

Среди экспериментальных образцов поляроидом был номер 5.

 

2 *. (5) В другом ящике той же лаборатории лежали вперемешку плоские зеркала и сферические зеркала с большим радиусом кривизны. Как их отделить друг от друга?

Решение:

Положение изображения объекта, видимого сквозь полупрозрачное сферическое зеркало, зависит от положения этого зеркала. Поэтому при небольшом поперечном смещении сферического зеркала все объекты, видимые сквозь него, сдвигаются, тогда как для плоского зеркала положения изображений фиксированы.

Среди экспериментальных образцов сферическим было зеркало под номером 1.

 

3. (5) Плоскость колебаний очень длинного маятника медленно поворачивается вследствие вращения Земли. Вернется ли маятник к своей первоначальной плоскости колебаний через сутки? Если нет - то в какой плоскости он окажется?

Решение:

Плоскость колебаний маятника Фуко в системе координат, связанной с Землей, поворачивается вследствие действия сил Кориолиса. Рассмотрим предельные случаи. На экваторе силы Кориолиса отсутствуют, и плоскость колебаний маятника неизменна. На полюсе можно считать, что плоскость колебаний маятника неподвижна в инерциальной системе отсчета, а Земля относительно нее вращается – и за сутки делает полный оборот. Другими словами, на полюсе плоскость колебаний маятника через сутки вернется в прежнее положение. Очевидно, между этими двумя предельными случаями должен быть плавный переход, что означает, что во всех прочих точках земной поверхности за сутки плоскость колебаний маятника Фуко сделает только часть полного оборота и не вернется в исходное положение через сутки.

 

4. (4) Для определения интенсивности метеоритного потока трое астрономов наблюдают за одной и той же областью неба, считают падающие звезды и записывают время падения каждой. Однако после часа наблюдения у каждого из них получились разные результаты: каждый из них пропустил часть метеоритов, а некоторые из них, возможно, были пропущены всеми. Предложите процедуру определения истинного числа упавших метеоритов.

Решение:

Вероятность регистрации метеорита каждым из наблюдателей определяется соответствующим коэффициентом , зависящем от его внимательности. Если полное число метеоритов , то количество метеоритов, замеченных -м наблюдателем, можно найти по формуле . Кроме того, легко найти количество метеоритов, зафиксированных всеми тремя наблюдателями - оно связано с полным числом метеоритов соотношением . Из этих двух формул легко видеть, что полное число метеоритов может быть найдено из экспериментальных данных по формуле

 

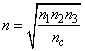
5. (3) С какой скоростью необходимо бежать от одного динамика к другому, чтобы слышать музыку, подаваемую на эти динамики с одного и того же магнитофона, одновременно в двух тональностях.

Решение:

Сдвиг частоты, вызванный движением относительно источника звука, определяется эффектом Доплера:

.

Разность частот мелодий, приходящих от двух динамиков, оказывается в два раза больше. С другой стороны, отношение частот двух соседних тональностей соответствует музыкальному интервалу в один полутон, то есть равно корню двенадцатой степени из двух (так как октава соответствует изменению частоты в два раза и состоит из двенадцати полутонов). Таким образом, скорость, с которой необходимо бежать, определяется из соотношения

,

откуда, считая, что скорость звука м/с, получаем м/с, то есть скорость, вполне допустимую для бегуна на короткие дистанции.

 

6. (3) Возможно ли повернуть поляризацию пучка света, распространяющегося в определенном направлении, только при помощи зеркал?

Решение:

Вполне возможно, если путь, который проходит свет, оказывается не лежащим в одной плоскости. Для демонстрация этого явления, называемого эффектом геометрической фазой, вытяните руку, сжатую в кулак, перед собой и поднимите вверх большой палец. Поднимите руку вверх, потом вытяните ее в сторону и, наконец, верните в первоначальное положение. В результате произведенных действий большой палец оказался в горизонтальном положении. Если сопоставить направление руки с направлением распространения света, а ее повороты - с отражением этого света в зеркалах, то направление большого пальца будет соответствовать направлению поляризации света, которое в процессе трех отражений повернулось на прямой угол.

 

7. (5) Возможно ли при помощи двух зеркал направить луч лазера (первоначальное направление луча фиксировано) вдоль прямой, проходящей через две маленькие дырочки? Опишите алгоритм, позволяющий это реально проделать.

Решение:

Очевидно, с помощью двух зеркал любой луч можно направить вдоль прямой g, проходящей через обе дырочки-диафрагмы. Для выполнения этой процедуры в экспериментальных условиях поставим одно из зеркал на прямую g, а с помощью другого зеркала направим световой луч на точку, являющуюся пересечением плоскости первого зеркала и прямой g. Теперь повернем первое зеркало относительно именно этой точки так, чтобы отражение луча прошло через обе диафрагмы. Задача выполнена.

 

8. (5) Как известно, свет состоит из фотонов. В результате так называемого параметрического рассеяния света в нелинейном кристалле фотоны возникают строго попарно и разлетаются в двух определенных направлениях. На пути каждого из них стоит фотодетектор, регистрирующий фотон с определенной вероятностью, называющейся его квантовой эффективностью. Опишите процедуру экспериментального определения квантовых эффективностей каждого из фотодетекторов.

Решение:

Задача практически эквивалентна задаче №4: так как два фотона появляются одновременно, они соответствуют одному и тому же метеору, который могут зарегистрировать два наблюдателя-фотодетектора. Также, как и в четвертой задаче, если полное число появляющихся пар фотонов , то количество фотонов, зарегистрированных -м фотодетектором , где - квантовая эффективность фотодетектора. Если использовать схему совпадений, дающую отсчет каждый раз, когда на нее одновременно с обоих фотодетекторов приходит фотоимпульс, то количество зарегистрированных ею совпадений будет связано с полным числом пар фотонов соотношением . Отсюда, квантовые эффективности фотодетекторов могут быть найдены по формулам

.

 

9. (3) Для Ферми-операторов плотности установлены правила умножения

Доказать тождества:

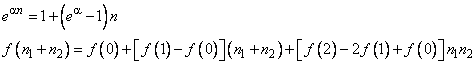
Решение:

Раскладывая в ряд Тейлора, получаем .

Для доказательства второго тождества также разложим произвольную функцию в ряд Тейлора около нуля:

.

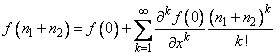Учитывая, что

, ,

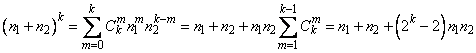получаем

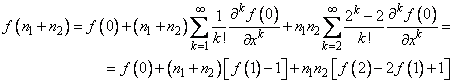, ч.т.д.

 

10. (3) В диэлектрическом слое связь между векторами электрического смещения и электрического поля имеет вид:

,

где - диэлектрическая проницаемость, а - кубическая восприимчивость. К слою приложено перпендикулярное к плоскости слоя однородное электрическое поле , причем . Найти поле внутри слоя.

Решение:

Так как внутри слоя нет свободных зарядов, электрическое поле в нем постоянно. Его величина должна быть найдена из условия равенства нормальных компонент вектора электрического смещения внутри и вне слоя, которое имеет вид кубического уравнения:

.

Учитывая малость нелинейности, в нулевом приближении , а в первом -

.

---

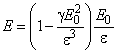* Материалы для экспериментальной проверки гипотез находятся у организаторов олимпиады. Желательно указать в ответе не только способ, но и результат его применения, то есть номера поляроида и сферического зеркала среди имеющихся стекляшек.